- Axis
- 패스트캠퍼스 #포트폴리오 #직장인자기계발 #환급챌린지 #포트폴리오챌린지 #패스트캠퍼스후기 #초격차패키지 #오공완
- math
- #패스트캠퍼스 #패캠챌린지 #수강료0원챌린지 #패캠챌린지 #직장인인강 #직장인자기계발 #패캠인강후기 #패스트캠퍼스후기 #환급챌린지 #본인이선택한강의명
- CP
- Computer science
- randn
- Counting
- Dim
- SUAPC
- argmax
- probability
- probability theory
- maths
- dims
- Discrete
- cs-theory
- laplace
- pytorch
- sinchon icpc
Piico의 일상
Day 3: Chapter 3. 왜 우리는 인공 신경망을 공부해야 하는가? (Part I) 본문
오늘의 공부: Ch 3-1에서 3-5까지
내용이 많아서 바로 시작 할께요~
TIL...
오늘 배운 내용들:
- weight & biases in DL
- linear regression
- gradient descent
- weight initialization (LeCun, Xavier, He)
- stochastic gradient descent
1. Weights and biases:
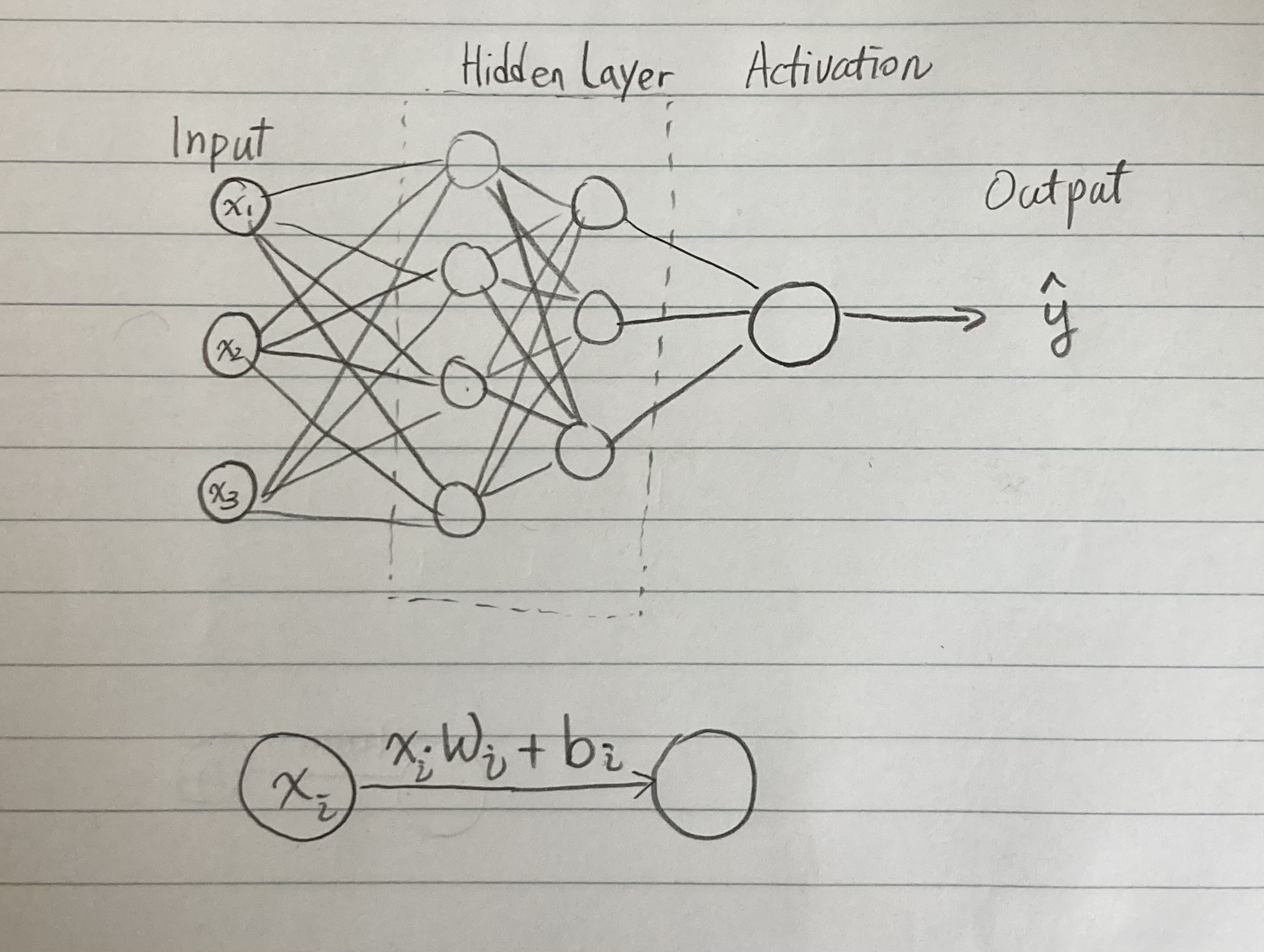
- 인공 신경망은 input layer -> hidden layer -> activation layer -> output 으로 이뤄져 있다.
- Input은 x로 표현하고 최종 결과는 y hat(prediction)이다.
- Hidden layer의 구조는 상황에 따라 다르게 쓸 수 있고 deep learning을 돌리다 보면 거기에 있는 weights and biases는 저절로 계산이 되는 과정이다. Deep learning model을 training완료하고 이 weights and biases를 잘 저장해 놓으면, 그 알고리즘은 저장됐고 다른 사람 하고도 공유하여 활용이 가능하다.
- 한 노드에서 다른 노드에 가는 과정에서 x * w + b = next_x가 되어 이어가면 된다.
- Activation은 prediction / output이 나오기 전에 정리를 해주는 함수이다. 예를 들어 Linear function (y=x), unit step function, Sigmoid, ReLU등이 있다.
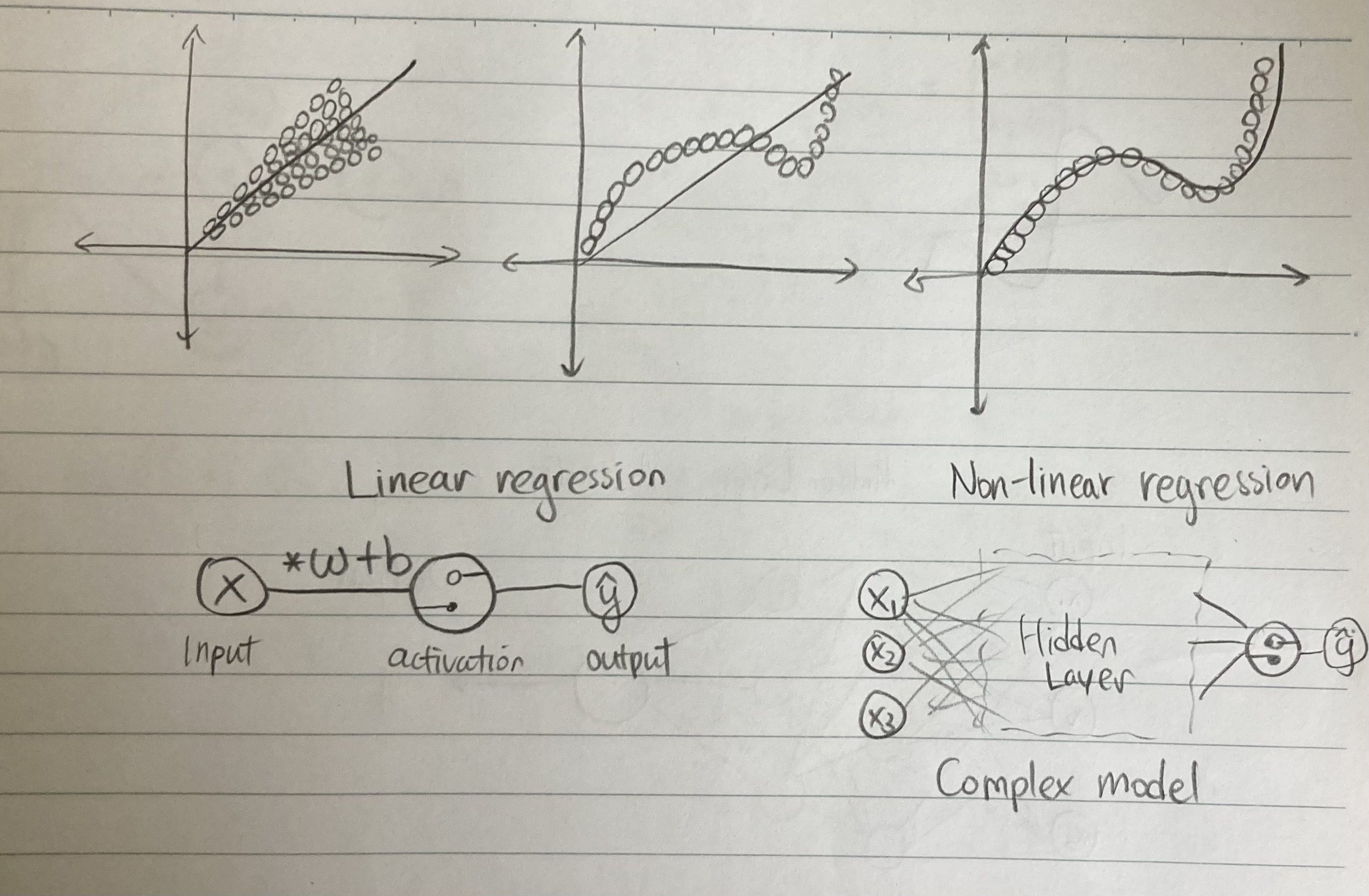
2. Linear regression (선형회귀):
Linear regression이란 인풋데이터에 대해 error를 최소로 줄이는 "선"을 그리는 것이다.
그럼 뭐 할 때 쓰이는데?
회귀는 데이터에 의존해 처음 보는 입력에 대해서도 적절한 출력 (prediction) 을 얻기 위함이다.
간단한 input -> activation function -> output로 만들면 선형회귀가 되는거다.
공식은 x * w + b이다. 하지만 여러 노드와 레이여가 있으면 선형회귀 뿐만 아니라 아주 intricate한 곡선을 만들 수 있다.
Weights and biases의 update에 따라 선이 곡선으로 변하고 더 정확한 prediction을 해낼 수 있다. weights가 올라가면 slope가 조금 꺾인다고 생각 할수 있다. 밑에 있는 그림을 참고해 주세요. Non-linear regression에서 graph가 꺾일 수 있는 것은 그 weights and biases의 결과이다.
Weights and biases을 update하려면 loss function이 필요하다. Loss function은 error를 최대한 줄일 수 있는 함수이다. 강의에서 언급한 MSE (mean squared error)는 선형회귀의 일종이다.
Mean squared error는 낱개의 error=y-y_hat를:
- 제곱해 준다 -> 제곱을 안하면 error_1=-1, error_2=1같은 상황은 Loss가 없는걸로 계산되서 update할께 없다. 여기서 absolute value를 안쓰는 이유는 제곱이 더 민감하기 때문이다 (이는 그래프를 보면 어느정도 알 수 있다)
- 그리고 n개의 (error)^2들을 합해서 n으로 나눈다... 그 이유는 n으로 안나누면 숫자가 너무 커지는 이유가 있다
3. Gradient descent vs stochastic gradient descent:
GD는 고질적인 문제 2개가 있다:
- 너무 느리다... (모든 error를 신중하게 계산 해야 하니)
- Local minimum에 빠질 수 있다... 빠지면 나오질 못한다...
| Gradient descent | Stochastic gradient descent | |
| 특징 | Epoch마다 모든 error에 대해 전부 계산한다 | 낱개의 error를 "주머니"에서 꺼내고 그것으로 loss를 계산한다 |
| 문제 1 (완화 방안 1) | 계산이 느리다 | 계산이 빠르다 |
| 문제2 (완화 방안 2) | 항상 Local minimum에 빠질 수 있다... 빠지면 나오질 못한다... | 낱개의 error를 loss로 계산하니 신중하진 않고 '튀'는 현상이 있다. |
4. Weight initialization은 쉽게 말해 일반적으로 0으로 쓰면 local minimum에 빠질수 있어 random initialization이 필요하다. 자세한 수학적 정의는 LeCun, Xavier, He라는 3연구자의 핵심연구에 의한 발견이다.


감사합니다~
'딥러닝 (Deep Learning)' 카테고리의 다른 글
| Day 6: Chapter 4-2 Backpropagation, 깊은 인공신경망의 학습 (0) | 2023.02.25 |
|---|---|
| Day 5: Chapter 4-1 MLP, 행렬과 벡터로 나타내기 & 왜 non-linear activation 중요할까? (0) | 2023.02.24 |
| Day 4: 왜 우리는 인공 신경망을 공부해야 하는가? Part 2 (0) | 2023.02.23 |
| Day 2: 왜 현재 AI가 가장 핫할까? (0) | 2023.02.21 |
| Day 1: 딥러닝을 위한 기초 수학 (0) | 2023.02.20 |




