- probability theory
- Computer science
- SUAPC
- cs-theory
- Counting
- Dim
- pytorch
- Discrete
- sinchon icpc
- randn
- laplace
- math
- CP
- Axis
- argmax
- maths
- #패스트캠퍼스 #패캠챌린지 #수강료0원챌린지 #패캠챌린지 #직장인인강 #직장인자기계발 #패캠인강후기 #패스트캠퍼스후기 #환급챌린지 #본인이선택한강의명
- 패스트캠퍼스 #포트폴리오 #직장인자기계발 #환급챌린지 #포트폴리오챌린지 #패스트캠퍼스후기 #초격차패키지 #오공완
- dims
- probability
Piico의 일상
Day 11: Chapter 1-20 MAP, MLE vs. MAP비교 본문
오늘 공부한 내용은 Ch.1-19, 1-20입니다:
Ch.1-19 MLE (maximum likelihood estimation)
Ch.1-20 MAP (maximum a posteriori)
Ch 5-5(softmax를 이용한 multiclass classification)를 듣다가 MAP라는 콘셉트가 나와서 강의가 이해가 안 돼 수학 파트를 찾아봤습니다. 아직 공부 안 한 MLE 하고 MAP파트를 봐야겠네요! 레벨 2 내용이라 MLE에 대한 이해도 잘 돼있어야 이해가 되는 나름 어려운 수준이네요.
1. MAP이 뭔가요?
MAP (maximum a posteriori)는 P(x | z)인 posterior의 maximum을 찾는 것입니다. MLE (maximum likelihood estimation)는 likehood를 maximum으로 찾는 듯이 이번에는 posterior에 대한 최댓값을 찾는 것인데 도대체 posterior가 뭘까요?

Likehood review
Likelihood의 정의는 P(z | x)입니다. 주머니에서 공 꺼내는 비유 생각 나시죠? 조건부는 같은 조건하에 칠한 안 칠한 공이고 likelihood는 조건이 다른 상황에 칠한/안 칠한 공의 확률이었죠?
Posterior
Posterior의 정의는 P(z | x) * P(x) / P(z)입니다. 눈치 채셨나요?
P(z | x) * P(x) / P(z)안에 likelihood인 "P(z | x)"가 들어갑니다. 그래서 posterior는 그냥 P(z | x)에다 P(x) / P(z)를 곱한 것입니다. 그래서 posterior는 P(x | z) = P(z | x) * P(x) / P(z).
Proof
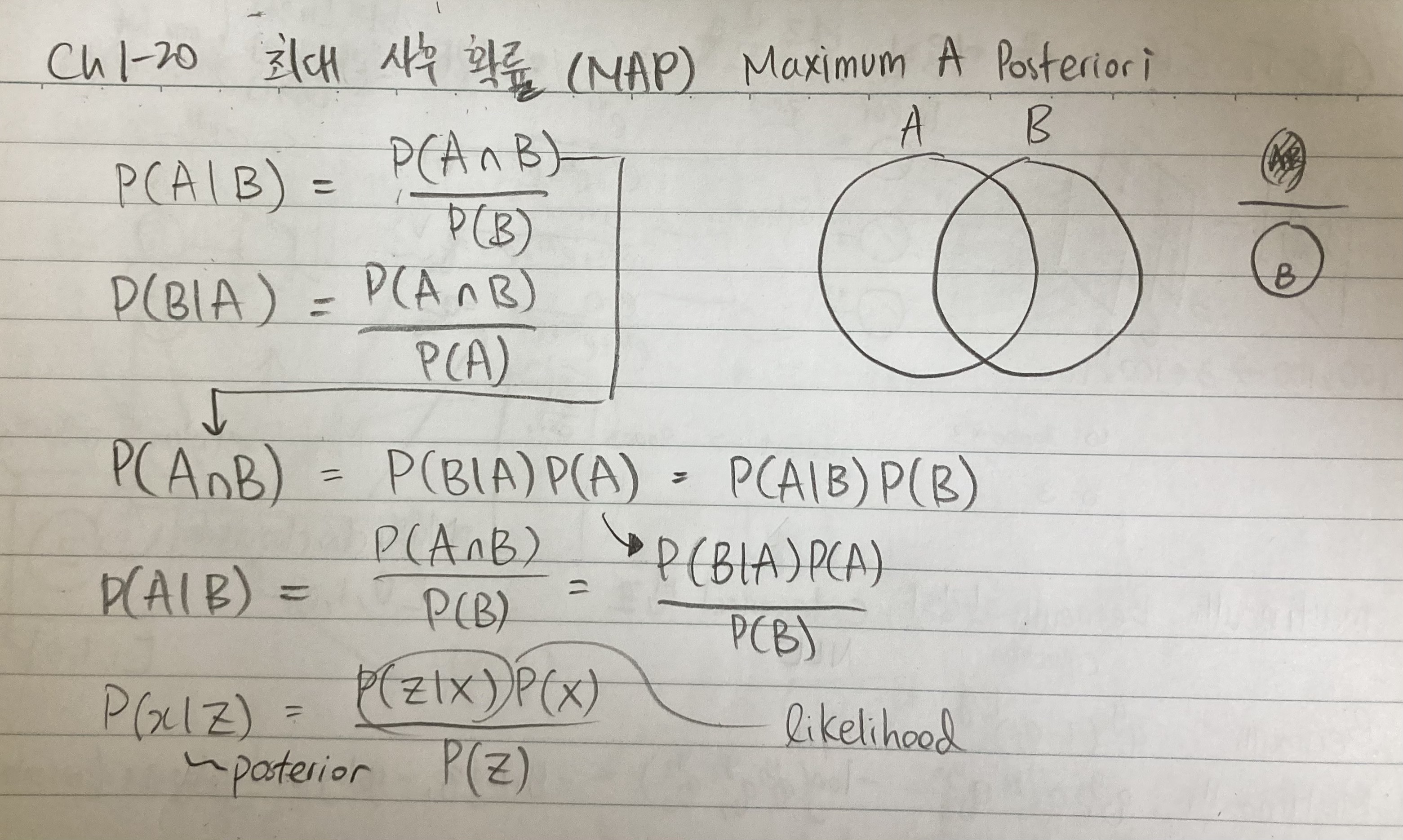
Proof는 이런 과정을 거칩니다:
1. P(A | B) = P(A ∩ B) / P(B) 또는 P(B | A) = P(A ∩ B) / P(A)가 있습니다.
(1)을 살짝 변형하면 (분모를 곱하면) 식이 이렇게 바뀝니다:
2. P(A ∩ B) = P(A | B) * P(B) 또는 P(A ∩ B) = P(B | A) * P(A)
여기서 (1)에서의 P(A ∩ B)에 다시 (2)을 대체하면 이렇게 됩니다:
3.a P(A | B) = P(A ∩ B) / P(B)
3.b P(A | B) = P(A ∩ B) = P(B | A) * P(A) / P(B)
이런 결과에다 A와 B를 x와 z로 대체하면 우리가 원하는 posterior를 계산 했습니다.
2. MLE 하고 MAP는 어떻게 차이 날까요?
오른쪽에 있는 사진 노트를 보면 증명과정을 기제 했습니다.
P(x | z) = P(z | x) * P(x) / P(z)와 P(z | x)의 차이는 결국 P(x) 하나의 차이가 되겠습니다.
다음 사진에 맨 오른쪽에 나타나는 e의 지수가 다른 걸 볼 수 있고 그 부분이 실직적인 차이가 되겠습니다.
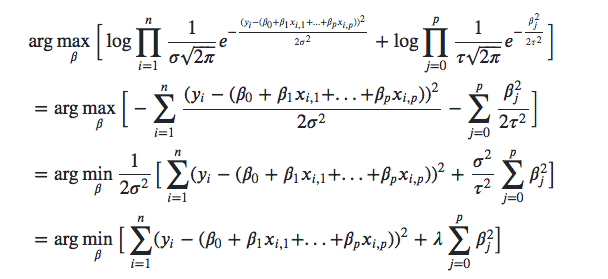

'딥러닝 (Deep Learning)' 카테고리의 다른 글
| Day 13: Ch.1-21 정보 이론 기초 (마지작 수학 파트) (0) | 2023.03.04 |
|---|---|
| Day 12: Chapter 5-4 ~ 5, MLE그리고 softmax를 이용한 다중 분류 (0) | 2023.03.03 |
| Day 10: Chapter 1-19 MLE (최대 우도 추정)에 대해 (0) | 2023.03.01 |
| Day 9: Chapter 5-3, MSE를 그대로 쓰면 안 되나? 왜 logistic regression이 더 필요한가? (0) | 2023.02.28 |
| Day 8: Chapter 4-3, 5-1, 5-2 선형분류와 sigmoid (0) | 2023.02.27 |




